Capitolo 6

Analisi della Regressione

L'analisi di regressione è un approccio per modellare la relazione lineare tra due variabili.

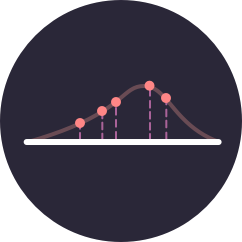
Metodo dei minimi quadrati

L'approccio alla regressione dei minimi quadrati ordinari (in inglese OLS: Ordinary Least Squares) consente di stimare i parametri di un modello lineare. L'obiettivo di questo metodo è determinare il modello lineare che minimizza la somma degli errori al quadrato tra le osservazioni in un insieme di dati e quelle previste dal modello. Esplora il metodo OLS attraverso i quattro "infami" dataset contenuti nel Quartetto di Anscombe.

Scegli uno dei quartetti da investigare.

Trascina e rilascia dati di punti per capire come questo ha effetto sulla linea OLS.

Clic su una colonna della tabella di regressione per capire di più in merito a questo parametro.

	$\displaystyle{n}$	$\displaystyle{\bar{\cssId{xMEAN}{x}}}$	$\displaystyle{\bar{\cssId{yMEAN}{y}}}$	$\displaystyle{\hat{\cssId{BETA0}{B_{0}}}}$	$\displaystyle{\hat{\cssId{BETA1}{B_{1}}}}$	$\displaystyle{SSE}$
Modello

$n$ è la dimensione del campione. Si tratta semplicemente del numero di punti di dati nel dataset fornito.

$\bar{x}$ è il valore medio dei dati di X. È definito matematicamente in questo modo:

$$\bar{x} = \sum_{i=1}^{n}\dfrac{x_{i}}{n}$$

$\bar{y}$ è il valore medio dei dati di X. È definito matematicamente in questo modo:

$$\bar{y} = \sum_{i=1}^{n}\dfrac{y_{i}}{n}$$

$\hat{B_{0}}$ è la Y intercettata dalla linea di regressione. La stima attuale ha una varianza di __. È definita matematicamente in questo modo:

$$\hat{B_{0}} = \bar{y} - \hat{B_{1}}\bar{x}$$

$\hat{B_{1}}$ è la pendenza della linea di regressione. La stima attuale ha una varianza di __. È definita matematicamente in questo modo:

$$\hat{B_{1}} = \dfrac{S_{xy}}{S_{xx}}$$

$SSE$ è la somma dei quadrati dei residui (in inglese la somma dei quadrati degli errori). È definita matematicamente in questo modo:

$$SSE = \sum_{i=1}^{n}\Big{(}y_{i} - \big{(}\hat{B_{0}} + \hat{B_{1}}x_{i}\big{)}\Big{)}^{2}$$

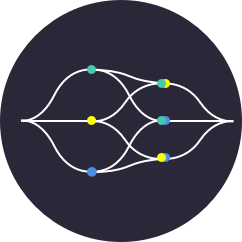
Correlazione

La correlazione è una misura della relazione lineare tra due variabili. È definita per un campione come segue ed ha valore compreso tra +1 e -1 inclusi:

$$r = \dfrac{s_{xy}}{\sqrt{s_{xx}}\sqrt{s_{yy}}}$$

$s_{xy},s_{xx},s_{yy}$ sono definite come:

$$\begin{align*} s_{xy} &=\sum^n_{i=1} (x_i-\bar{x})(y_i-\bar{y})\\ s_{xx} &=\sum^n_{i=1} (x_i-\bar{x})^2\\ s_{yy} &=\sum^n_{i=1} (y_i-\bar{y})^2 \end{align*}$$

Può anche essere intesa come il coseno dell'angolo formato dalla linea ordinaria minima quadrata determinata in entrambe le dimensioni variabili. Esplora questo concetto attraverso il famoso dataset dei fiori Iris di Edgar Anderson.

Scegli quale specie vuoi conoscere.

Clic su una cella della matrice di correlazione per visualizzare la correlazione fra questi tratti.

	Lunghezza Sepalo	Larghezza Sepalo	Lunghezza Petalo	Larghezza Petalo
Lunghezza Sepalo
Larghezza Sepalo
Lunghezza Petalo
Larghezza Petalo

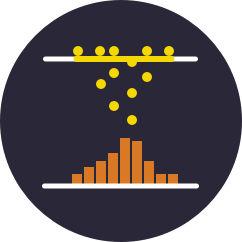
Analisi della Varianza

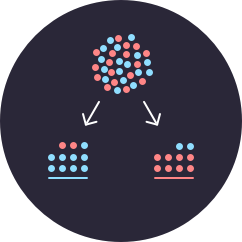
L'Analisi della Varianza (ANOVA) è un metodo statistico per testare se gruppi di dati hanno la stessa media. L'ANOVA generalizza il test-t per due o più gruppi comparando la somma della radice degli errori all'interno e fra gruppi.

Scegli uno di questi dataset da investigare

Trascina i rilasci i dati puntuali per esplorare come questo ha affetto nel risultato del test di ANOVA

Clic su una colonna della tabella ANOVA per conoscere di più riguardo questo parametro.

	$\displaystyle{SSE}$	$\displaystyle{df}$	$\displaystyle{MS}$	$\displaystyle{F}$	$\displaystyle{p}$
Trattamento
Errore
Totale

$SSE$ è una abbreviazione (inglese) per la somma dei quadrati degli errori che è la somma dei quadrati residui. SSE è definita matematicamente in questo modo:

$$SSE = \sum_{i=1}^{n} \big{(}y_{i} - \bar{y}\big{)}^{2}$$

$df$ è una abbreviazione in inglese per i gradi di libertà relative al numero di dati puntuali. Si definisce matematicamente in questo modo:

$$df = n - 1$$

$MSE$ - errore quadratico medio (in inglese Mean Squared Error, MSE) indica la discrepanza quadratica media fra i valori dei dati osservati ed i valori dei dati stimati. È definito matematicamente in questo modo:

$$MSE = \dfrac{SSE}{df}$$

$F$ è un test statistico che è definito in questo modo:

$$F = \dfrac{SST/(k-1)}{SSE/(n-k)} \sim f_{k-1,n-k}$$

$p$ è il valore p che è determinato dalla F statistica.

Scarica

	\(\displaystyle{n}\)	\(\displaystyle{\bar{\cssId{xMEAN}{x}}}\)	\(\displaystyle{\bar{\cssId{yMEAN}{y}}}\)	\(\displaystyle{\hat{\cssId{BETA0}{B_{0}}}}\)	\(\displaystyle{\hat{\cssId{BETA1}{B_{1}}}}\)	\(\displaystyle{SSE}\)
Modello

	\(\displaystyle{SSE}\)	\(\displaystyle{df}\)	\(\displaystyle{MS}\)	\(\displaystyle{F}\)	\(\displaystyle{p}\)
Trattamento
Errore
Totale

Capitolo 6

Analisi della Regressione

Metodo dei minimi quadrati

Correlazione

Analisi della Varianza

Prossimo