Capitolo 1
Probabilità di Base
Questo capitolo è un'introduzione ai concetti di base della teoria della probabilità.

Eventi Aleatori
Tutto ciò che ci circonda è casuale. La teoria della probabilità è lo strumento matematico che ci consente di analizzare eventi casuali in modo strutturato. La probabilità di un evento è un numero che indica quanto è fattibile il verificarsi di questo. Questo numero è sempre tra 0 e 1, dove 0 significa impossibilità, mentre 1 significa certezza.
Un tipico esperimento probabilistico è il lancio di una moneta, in cui ci sono solo due possibili risultati: testa (H) o croce (T). La probabilità di ottenere testa o croce al lancio della monetà è di 1 su 2. In una serie reale di lanci di monete, possiamo ottenere più o meno esattamente il 50% di teste o croci. Ma con l'aumentare del numero di lanci, la frequenza di uno dei due risultati è destinato, a lungo termine, ad avvicinarsi sempre di più al 50%.
Per una moneta ingiusta o ponderata, i due risultati non sono ugualmente probabili. È possibile modificare il peso o la distribuzione della moneta trascinando le barre di probabilità reali (a destra in blu) verso l'alto o il basso. Se assegniamo i numeri ai risultati, ad esempio 1 per le teste, 0 per le croci, abbiamo creato l'oggetto matematico noto come variable aleatoria.
Valore Atteso
Il valore atteso di una variabile casuale è il numero che tenta di catturare il centro della distribuzione di detta variabile casuale. Possiamo interpretarlo come la media di molti campioni indipendenti di quella distribuzione. Più precisamente, è definita come la somma ponderata di tutti i possibili valori nel supporto della variabile casuale, i cui pesi sono le probabilità di occorrenza di ciascuno dei valori
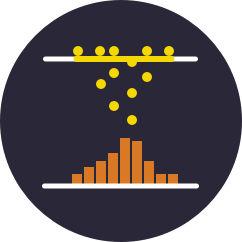
$$\text{E}[X] = \sum_{x \in \mathcal{X}}xP(x)$$Considera l'esperimento di lanciare un dado e osservare come la media campionaria converge verso il valore atteso di 3,5.
Cambia la distribuzione delle diverse facce del dado (rendendo così il dado "prevenuto" o "scorretto") regolando le barre blu in basso e guarda come cambia il valore atteso.
Varianza
Mentre il valore atteso fornisce una misura della centralità, la varianza di una variabile casuale quantifica la larghezza o l'estensione della sua distribuzione di probabilità. La varianza è la media dei quadrati degli scarti dei singoli valori dalla loro media aritmetica.
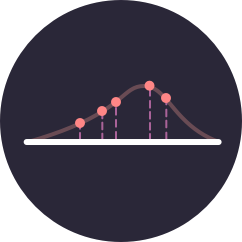
$$\text{Var}(X) = \text{E}[(X - \text{E}[X])^2]$$Pesca a caso carte da un mazzo di 10 carte. Mentre peschi le carte, nota che la media cumulativa delle differenze al quadrato (in verde) comincia ad assomigliare alla varianza (in azzurro).
Scegli le carte che vuoi includere nel mazzo facendo clic su ciascuna qui sotto.